Aperçus de la méthode

Physique

Apprentissage Machine

Présentation Générale

L'objectif de ce projet est de développer de nouvelles manières de modéliser le comportement de systèmes complexes, plus informatives, pour gagner en compréhension sur leurs comportements.

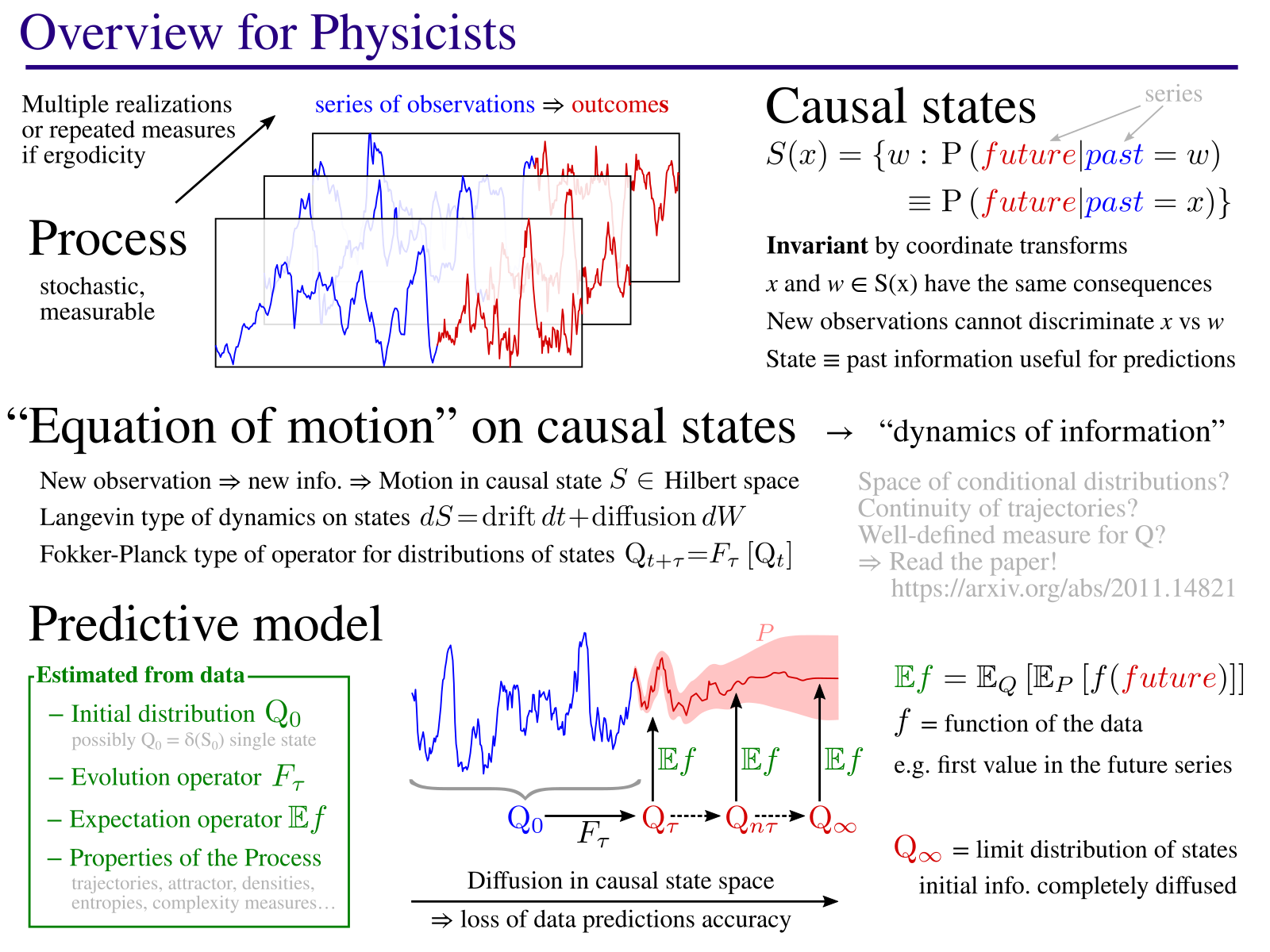
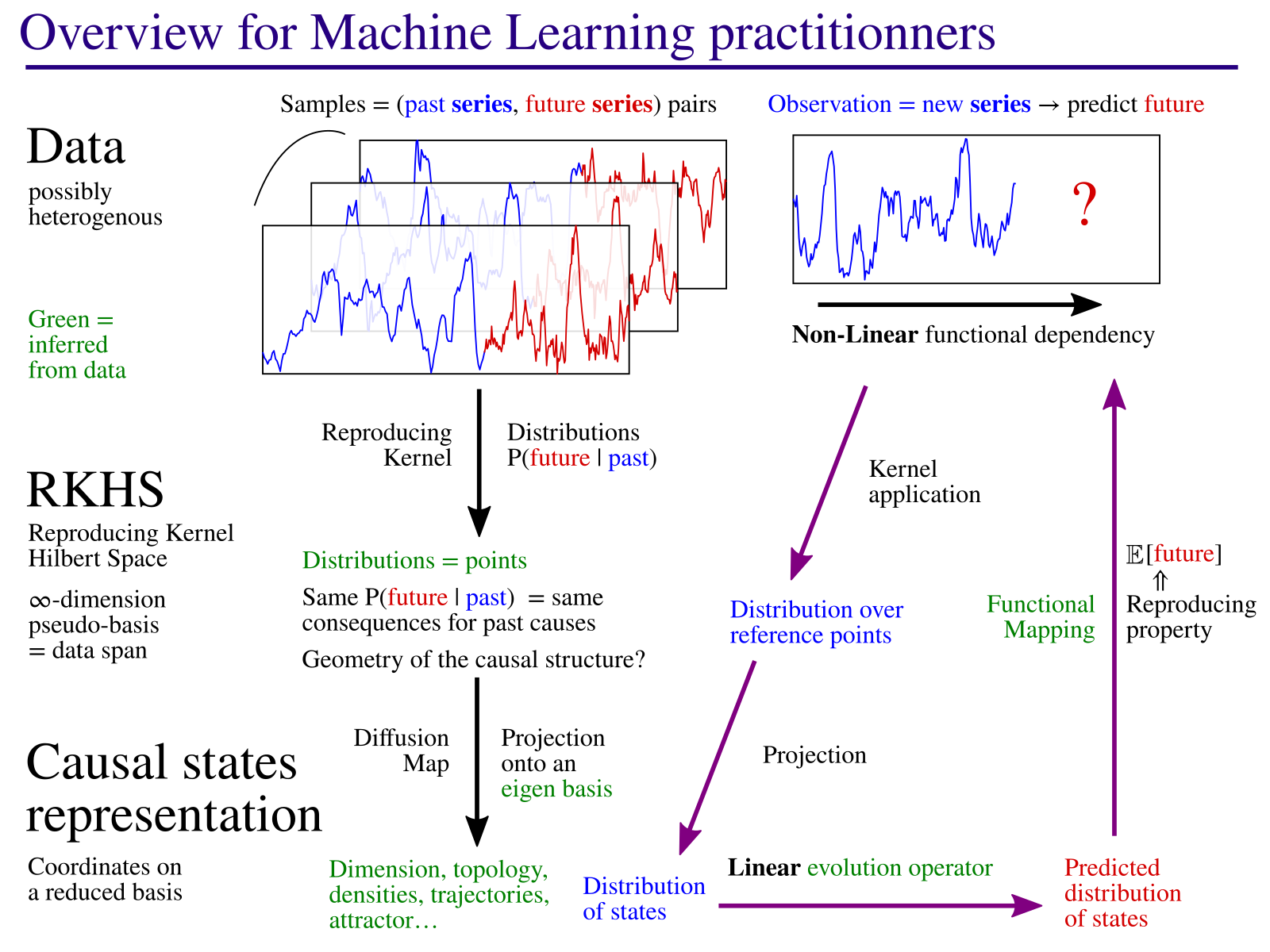
La méthode consiste à identifier des états causaux : des états qui, lorsque le système étudié s'y trouve, mènent toujours au même type de comportement. Le modèle consiste alors à décrire la dynamique de ces états, une « équation du mouvement » dans l'espace de ces états causaux. Cette équation décrit comment, partant d'une connaissance initiale basée sur les données observées, cette information connue est diffusée avec le temps. Comme vous pouvez le voir sur l'image à droite, la méthode permet aussi de trouver la structure géometrique sur laquelle évoluent les états causaux. Ceci correspond à un attracteur pour le cas d'un système chaotique (exemple dans le papier). Pour ce faire, la méthode identifie les paramètres importants (ici, 3 axes X,Y,Z) qui décrivent au mieux l'évolution des états causaux.

Ce cadre permet en théorie de quantifier des propriétés importantes d'un processus naturel. En effet, les états causaux sont par définition invariants par changement de coordonnées et sont une propriété intrinsèque du système étudié. Par exemple, il serait très utile de quantifier des échelles caractéristiques, comme le temps moyen pour que l'information initiale se diffuse au point que la qualité des prédictions est réduite de moitié. Ou encore, des mesures de complexité, comme la difficulté d'établir des prédictions en différents points de mesures. Peut-être plus important, en faisant varier l'échelle d'analyse, cette méthode a le potentiel pour trouver des motifs, des structures cachées au sein des données qui sont porteuses d'information.

C'est tout l'enjeu de l'analyse des systèmes complexes. Des systèmes, composés d'un grand nombre d'éléments parfois très simples en interaction, mais qui font apparaître à grande échelle des comportements inattendus. Citons par exemple des colonies de fourmis, des neurones, des réseaux d'interaction génomique, ou encore des couplages océan/atmosphère/végétation... Si on dispose des lois d'interaction de tous les éléments à petite échelle, on peut parfois réaliser un modèle de leur comportement global. Mais cette approche est rapidement limitée par la puissance de calcul nécessaire pour exécuter le modèle. L'approche proposée ici vise à reconstruire une dynamique, la dynamique de l'information contenue dans les mesures et qui est utile pour établir des prédictions. Avec cette dynamique, on peut espérer obtenir un modèle effectif du système étudié qui fonctionne à grande échelle, sans pour autant avoir besoin de modéliser chacun de ses éléments constitutifs. À noter qu'il n'est pas garanti que les prédictions obtenues soient aussi bonnes... la théorie indique qu'avec une quantité infinie de données le modèle est optimal mais, en pratique, on retombe rapidement sur des limites de puissance de calculs. D'autres modèles, plus simples, peuvent alors donner de meilleurs résultats d'un point de vue purement prédictif. En revanche, la méthode proposée apporte une meilleure compréhension du système étudié, de ses propriétés, que ne font pas les modèles plus simples.

Ce type d'approche et des variantes sont étudiées depuis des dizaines d'années par de nombreux groupes en physique non linéaire et en science des sytèmes complexes, en particulier celui de James P. Crutchfield, co-auteur du papier et initiateur du cadre théorique autour des états causaux depuis les années 1980. Des liens forts existent aussi avec la thermodynamique hors équilibre. En effet, qui dit transformation d'information dit relation avec la thermodynamique. Qui dit maintien d'une structure au cours du temps dit réduction d'entropie, donc consommation d'énergie. Mais précisement, pour la plupart des systèmes qui nous intéressent (atmosphère, cellule, fourmilière, etc), la dissipation d'énergie est un prérequis mais n'est pas toujours informative. Ce qui importe le plus, ce qui fait la fonction de l'objet à grande échelle, c'est le maintien de structures et leurs interactions au cours du temps. Un modèle comme celui proposé ici a le potentiel pour identifier et quantifier l'information contenue à différentes échelles. Il décrit aussi la façon par laquelle cette information est transformée.

Il va de soi que beaucoup reste à faire. Le modèle proposé ici n'a pas la prétention de résoudre tous ces problèmes... juste d'apporter un pas supplémentaire, en suivant le chemin ouvert par de nombreux groupes sur les sciences de la complexité, du chaos et de la physique non linéaire, pour mieux modéliser et comprendre les processus naturels.

N'hésitez donc pas à me contacter (adresse mail en bas de la page) si vous souhaitez discuter de ces sujets. En particulier, si vous cherchez une thèse, un post-doctorat voire même un poste permanent à l'Inria. Cela s'anticipe alors prenez contact assez tôt et voyons ce qu'on peut faire ensemble!

Exemple d'analyse : l'activité solaire

L'activité solaire est mesurée en notant le nombre de taches solaires qui apparaissent chaque mois. Les périodes d'activité suivent un rythme d'environ 11 ans. La prédiction de ces cycles (ou demi-cycles…) solaires est notoirement difficile. Pour tester l'algorithme et sa capacité à repérer des motifs à grande échelle, nous allons l'appliquer à la dynamique du soleil à long terme. L'algorithme est paramétré pour coller à l'échelle de temps caractéristique de 11 ans : il va analyser les relations entre les mesures sur 132 mois et celles sur les 132 mois suivants. Les données sont récupérées depuis le centre SILSO d'analyse de données solaires et le script d'analyse est disponible dans mon dépôt de sources.

Représentation 3D des états causaux inférés à partir des données du cycle solaire. L'image est dynamique et vous pouvez naviguer dans la structure. Les années des maximums solaires sont notées en bleu et les minima en noir.

La méthode propose une projection des états causaux sur un nombre réduits de paramètres les plus significatifs. Clairement les 2 paramètres X et Y encodent, ensemble, une période d'environ 11 ans ainsi que la phase dans cette période. Ce qui est rassurant, vu qu'il s'agit de la principale caractéristique macroscopique de ce processus.

Les trajectoires semblent toutes s'inscrire sur une structure conique. Mais quelle est la signification de Z, le paramètre de hauteur du cone ? Ce paramètre est clairement identifié comme important par l'algorithme qui le place en 3ème dimension, mais je ne pouvais pas déterminer sa signification. J'ai donc demandé aux experts du SILSO: il s'agit de la modulation des amplitudes sur de longues périodes, connue comme le cycle de Gleissberg. Et en effet, les dates sur les parties hautes et basses du cône correspondent à celles de cette modulation de basse fréquence ! Ceci démontre la capacité de l'algorithme à encoder la dynamique du processus, et non juste les dépendances statistiques immédiates.

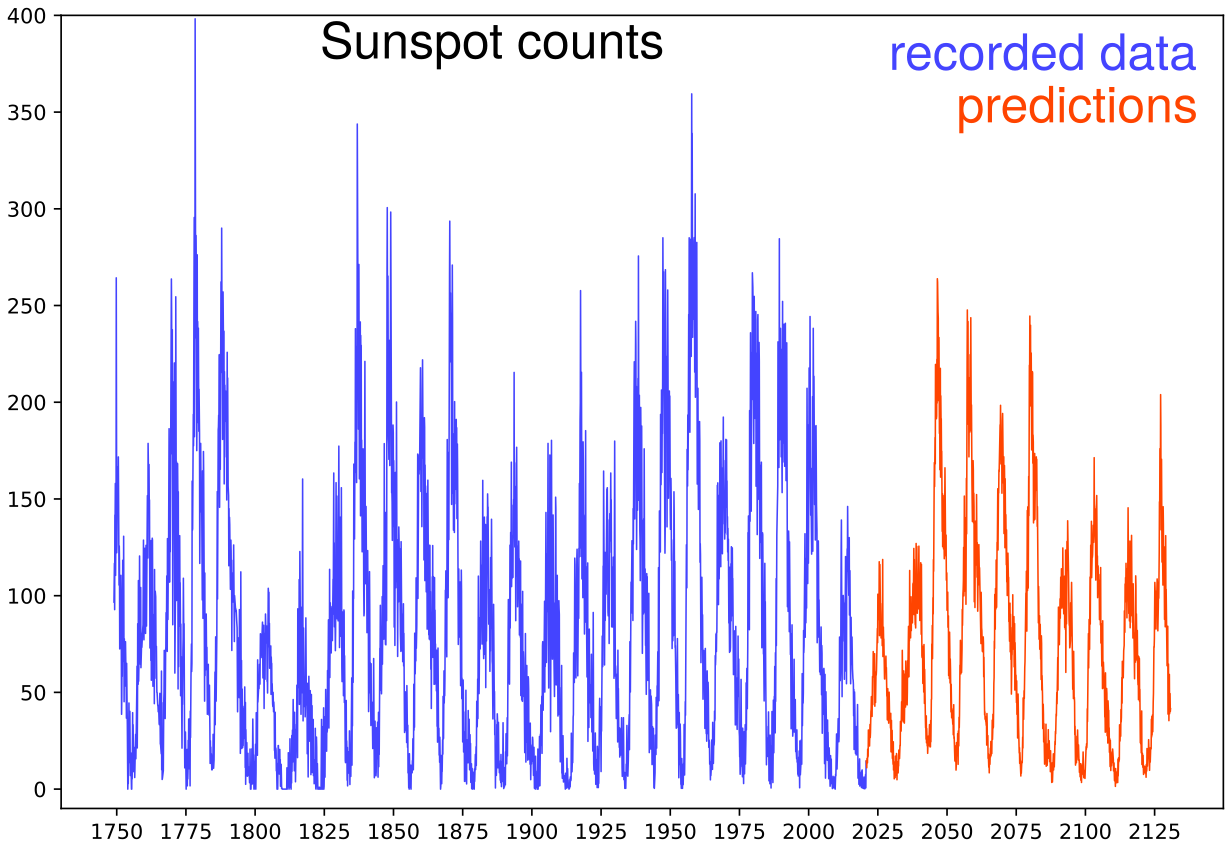
Prédictions obtenues par la méthode sur une période ridiculement longue. L'idée est de montrer le comportement de l'algorithme, qui propose une réalisation possible du processus. Il a un peu de mal avec les minima, mais dans l'ensemble la dynamique cyclique est bien respectée et la réalisation proposée semble plausible et cohérente avec les données précédentes. Y compris l'apparition d'un nouveau cycle de Gleissberg! Étant donné la difficulté bien connue de ce jeu de données, il serait illusoire d'accorder un quelconque crédit aux prédictions à plus d'un cycle. En termes de systèmes dynamiques, ces prédictions montrent juste une trajectoire possible sur « l'attracteur ». On pourrait se demander à quelle vitesse l'information initiale se diffuse, autrement dit à quel point les trajectoires divergent rapidement, mais ceci nous amènerait trop loin pour cet exemple d'illustration. Il faudrait aussi calibrer l'algorithme avec des experts si on souhaite obtenir des prédictions plus précises.

Article et code de référence

Une version preprint de l'article est disponible ici ainsi que sur ArXiv.org.

La dernière version du code source est disponible ici. Les scripts sont écrits en Python, avec un module C++ pour améliorer le temps de calcul (une version pure Python est en préparation – merci de me contacter si besoin est). Il n'y a pas de dépendances externes autres que celles fournies avec le code. Licence MIT : soyez libres d'en faire ce que vous voulez tant que vous créditez l'auteur !