Ce nouvel algorithme quantifie la différence entre les propriétés statistiques de chaque côté de chaque pixel. Il réalise un genre de filtre, capable de détecter des échelles caractéristiques spatiale (e.g. en pixels) et de données (e.g. en niveau de gris). L'algorithme n'est pas limité aux données scalaires, comme la luminosité d'une image. Il peut travailler directement sur des vecteurs ou de nombreux autres objets pour lequels un "noyau reproduisant" est défini. De même, il n'est pas spécifiquement limité aux images 2D. Voici quelques exemples d'applications, montrant la polyvalence de la méthode. Plus de détails sur l'algorithme sont donnés ci-dessous, ainsi que l'article correspondant.
Focus sur les petites ou les grandes variations



L'algorithme permet de spécifier une échelle caractéristique des changements recherchés dans les données. Par exemple, à une échelle de 1 niveau de gris (deuxième image), l'algorithme détecte les artefacts jpegs dans le ciel et autour du manteau. Les grandes variations de luminosité sont par contre complètement ignorées, ce qui pourrait être utile par exemple pour supprimer le bruit lié aux artefacts jpegs sans toucher aux zones de grand contraste. Ces dernières sont trouvées dans la troisième image, en spécifiant une échelle correspondante au contraste maximal noir/blanc, et donne un résultat proche de ce que ferait une détection de bord plus classique, basée sur les forts gradients de luminosité. Cette capacité de filtrer les petites ou les grandes variations rend l'algorithme très adaptable en fonction du contexte applicatif.
Bords entourant des motifs répétitifs

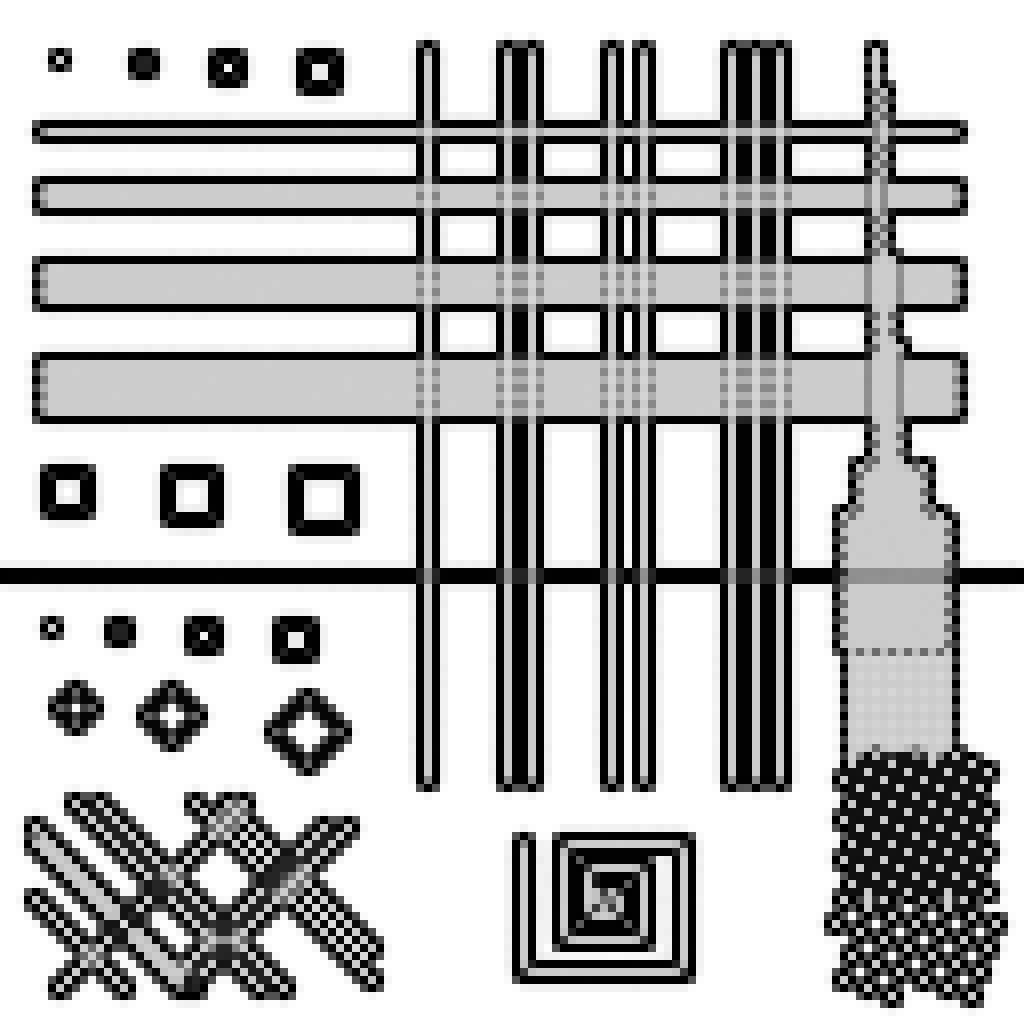
L'algorithme permet de spécifier une échelle spatiale, à laquelle les motifs sont reconnus et traités comme une texture unique. Ici, en utilisant une échelle d'un pixel, un bord est détecté autour, mais non à l'intérieur, des lignes horizontales séparée d'un pixel. De même pour les damiers à droite, où la différence est clairement visible entre ceux usant d'un motif répétitif à l'échelle d'un pixel (ils sont entourés d'un bord unique) et ceux plus bas qui utilisent un motif à sur plus large échelle (chaque point est considéré isolément). Cette technique fonctionne également en diagonale, cf en bas à gauche où un bord unique est défini autour des lignes séparées d'un pixel mais pas de celles séparées par deux ou plus pixels.
Inférence d'échelles caractéristiques


Quand on fait varier à la fois échelle spatiale et échelle de valeurs de données, on peut regarder à quelles échelles l'information extraite par les zones détectée est maximale. Ainsi, non seulement on peut détecter les zones « où il se passe quelquechose », là où l'information est concentrée, mais également en déduire les échelles pertinentes pour l'analyse de ces zones. Dans l'image ci-dessus, on peut ainsi retrouver les courants océaniques, avec des largeurs caractéristiques de 75 km (au centre de l'image) et pour des variations de 1°C.
Détection de bords en couleur


Par l'usage d'un noyau reproduisant, cet algorithme travaille directement sur des vecteurs, dont les espaces colorimétriques. Il incorpore donc l'information de couleur directement dans la détection de bords. On peut envisager d'autres vecteurs de données, comme des images multispectrales ou des bandes radar, ou encore d'autres espaces de valeurs non vectoriels (e.g. chaînes de caractères). L'image est un extrait de cette photographie prise par Thomas Bresson, sous Creative Commons - Attribution.
Comment ça marche
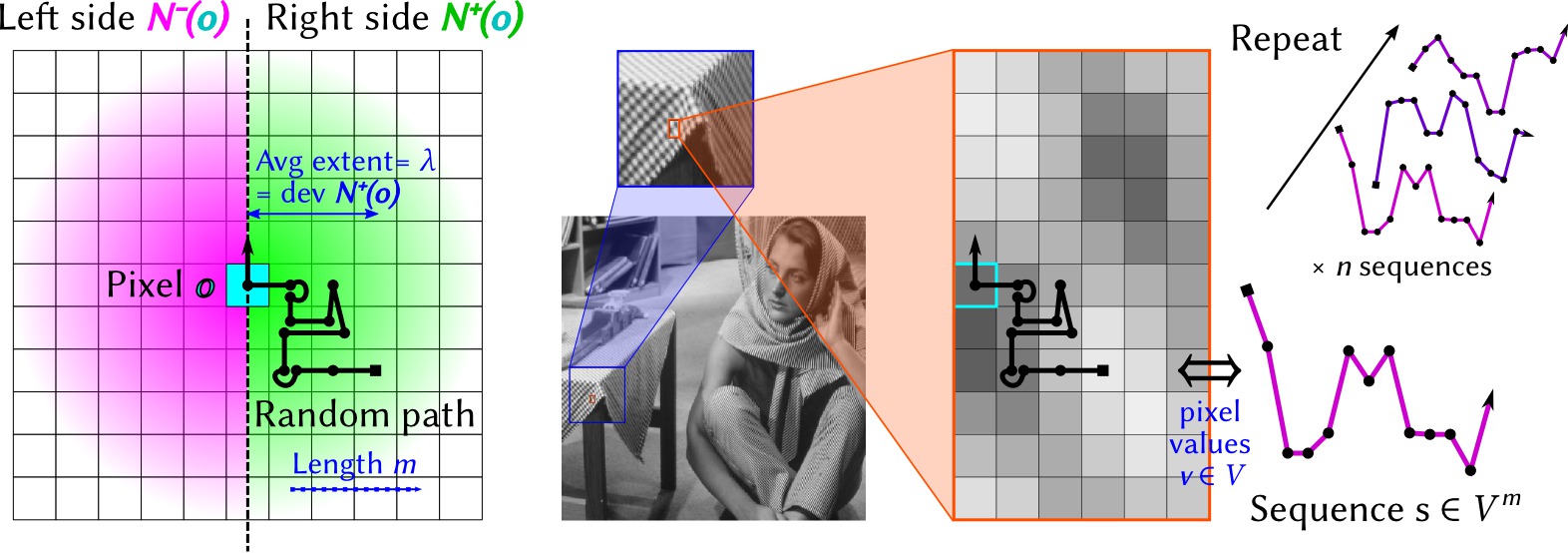
L'idée est de comparer les propriétés statistiques de chaque côté d'un pixel, puis de recommencer dans chaque direction souhaitée (e.g. horizontale, verticale et diagonales). On commence (gauche) par générer un chemin aléatoire de longueur m, qui, en moyenne, s'étend sur λ pixels. Cette échelle spatiale est également l'écart-type de la distribution des probabilités d'occurence de chaque pixel dans un des chemins (densité représentée en vert ou en rose). On prend ensuite les valeurs des pixels v∈V le long du chemin, afin de générer une séquence de valeurs dans Vm.
On considère alors une texture comme une distribution de probabilité dans Vm. Intuitivement, cette distribution décrit comment les valeurs des pixels évoluent dans la région considérée. En générant n séquences dans Vm, on peut construire un estimateur empirique de cette distribution de probabilité. L'astuce est d'exploiter une représentation de cette distribution dans un espace de Hilbert à noyau reproduisant, dans lequel l'estimateur empirique s'exprime très simplement. Un autre avantage est que la norme entre deux points dans cet espace quantifie directement la distance entre deux distributions de probabilités, soit, dans le cas qui nous intéresse, la différence entre les textures de chaque côté d'un pixel. La taille du noyau reproduisant définie l'échelle dans l'espace des valeurs de données, à laquelle la différence de texture est calculée.
Article et code
Une version preprint de l'article est disponible ici et sur ArXiv.org, ainsi que la présentation donnée en keynote session à la conférence Recent Advances in Electronics & Computer Engineering en janvier 2015.
Le code est maintenu comme sous-projet sur la gforge d'Inria, en attendant de livrer une version indépendante sur mon dépôt de sources à la publication de l'article. Il s'agit dans tout les cas d'un logiciel libre disponible en LGPL v2.1 ou plus recent

