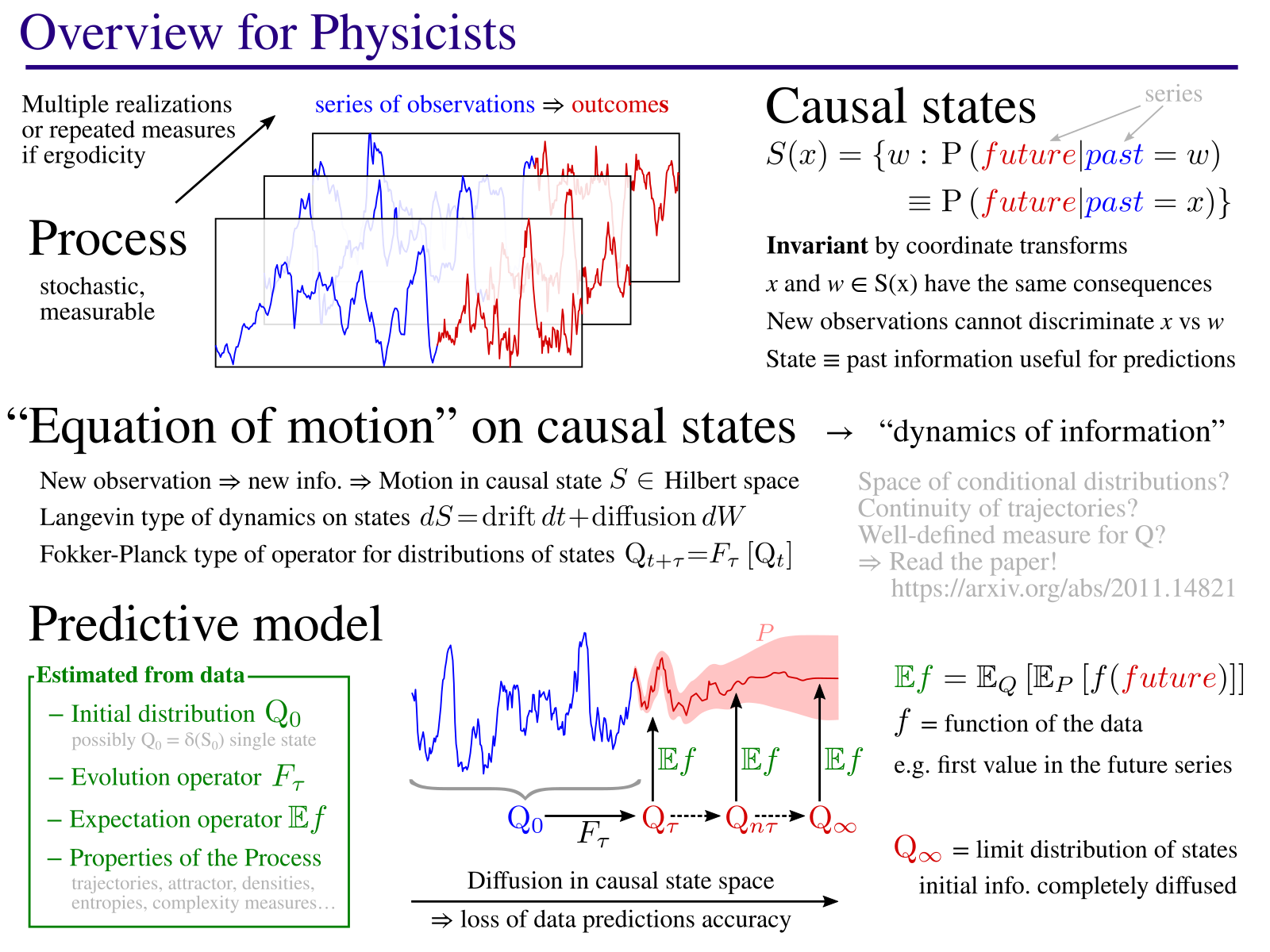
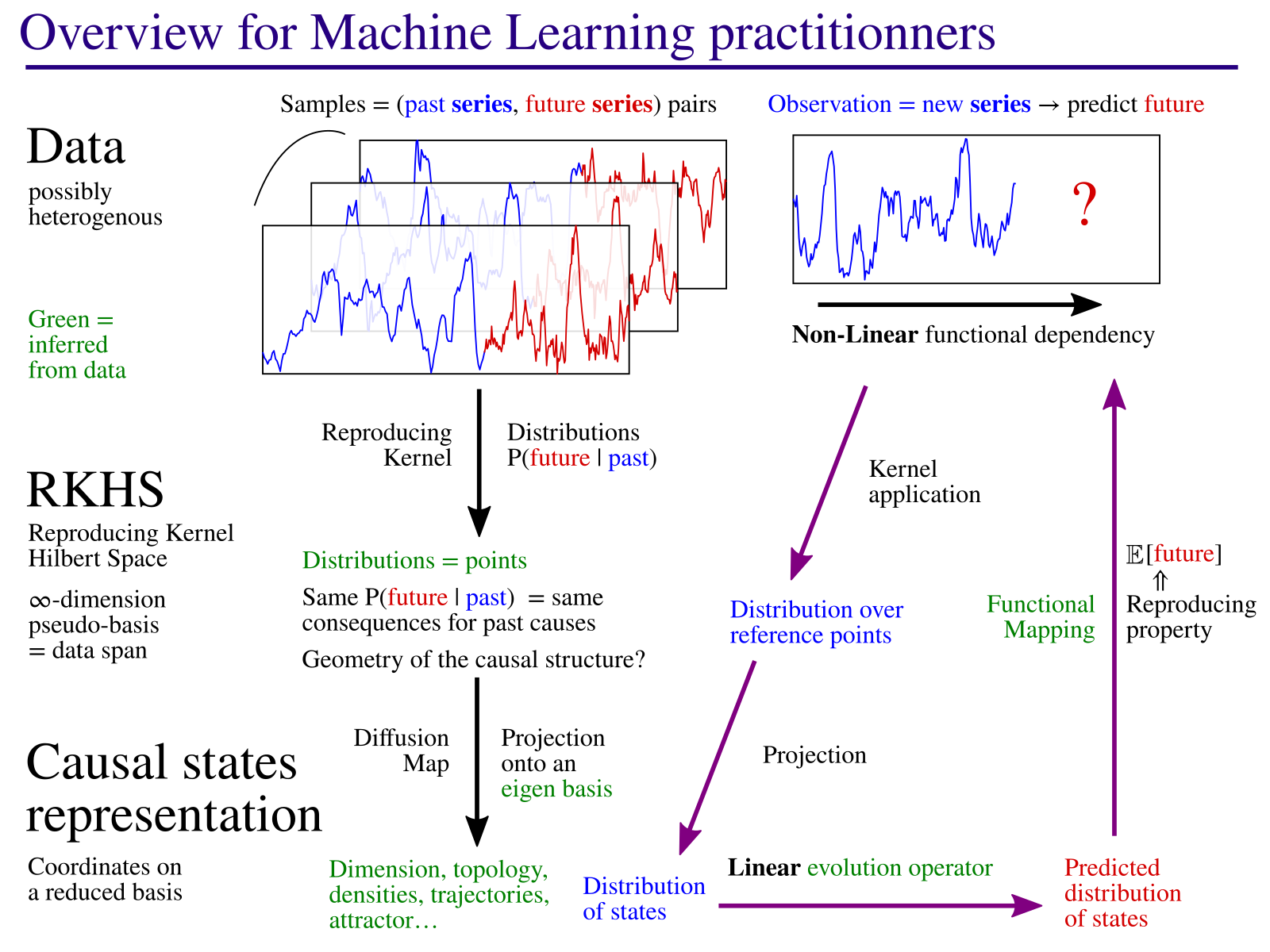
Overview of the method

Physics

Machine Learning

General Description

The goal of this project is to develop new approaches for modeling complex systems, more informative on their behavior.

The method consists in identifying causal states: states of a process which always lead to the same kind of behaviors. The model then describes the dynamic of these states, an “equation of motion” in the causal state space. This equation describes how, starting from initial knowledge from current observations, the known information is diffused with time. As you can see in the 3D image on the right, the method also identifies the geometric structure on which causal states evolve. This corresponds to an attractor in the case of chaotic dynamical systems (example in the paper). As part of this process, the method identifies the main parameters (here, 3 axes X, Y, Z) that best describe the evolution of the causal states.

This framework allows in theory to quantify some important properties of a natural process. Indeed, the causal states are by definition invariant by change of coordinates and they are an intrinsic property of the process which is studied. For example, it could be very useful to quantify characteristic scales, such as the mean time by which the initial information has diffused to the point that the prediction accuracy is reduced by half. Or measures of complexity, such as the difficulty to produce predictions from various measurement points. Perhaps more importantly, by varying the analysis scale, this method has the potential to identify hidden patterns in the data, the structures that bear information.

This is one of the main goal of complex systems analysis. Systems, comprised of a large number of – sometimes very simple – interacting elements, but which yield unexpected behaviors on large scales. Such systems could be ant colonies, neurons, genomic interaction networks, or maybe couplings between the ocean, the atmosphere and vegetation... If one knows the elementary laws describing all the interactions at small scale, it is sometimes possible to model and simulate the large scale behaviors. But this approach is quickly limited by the computational resources required to run such models. The approach proposed here aims at reconstructing an effective model of the system dynamics. Or, more precisely, the dynamics of the information contained in measurements which is useful for establishing predictions. With this model we can hope to effectively describe how the system evolves directly at large scale, without having to model each of its elementary constituents. Note though that it is not guaranteed that predictions are accurate... the theory indicates that the model is optimal with infinitely many observations but, in practice, we also reach computational limits pretty fast. Simpler models, easier to fit to data, may then provide better results from a purely predictive point of view. However, the proposed method estimates a whole new set of properties of the system and can bring understanding not available from simpler models.

This kind of approach and variants have long been studied by many groups in non-linear physics and complexity sciences. In particular, the group of James P. Crutchfield, co-author of the paper and inventor of the theoretical causal states framework since the 1980's. Strong links also exist with out of equilibrium thermodynamics. Indeed, information transforms are deeply linked with thermodynamics. Maintaining a structure through time implies a reduction of entropy, hence a dissipation of energy. But, precisely, for many systems of interest (the atmosphere, cells, ant colonies, etc), energy dissipation is a prerequisite and may not be very informative. What matters most, what makes the function of an object at large scales, is the persistence of structures and their interactions through time. A model such as what is proposed here has the potential to identify and quantify the information contained at different scales. It also describes how that information is transformed.

Obviously, much remains to be done. The model proposed here does not have the ambition to solve all these issues... it is just another step – following the path shown by many groups in complexity, chaos and non-linear sciences – towards a better understanding and modeling of natural processes.

Do not hesitate to contact me (email at the bottom of the page) if you wish to discuss these topics. In particular, if you are looking for a PhD, a post-doctoral contract or a permanent position at Inria. This needs to be prepared in advance, so contact me as soon as you can if you are interested and let's see what we can do together!

Example: analyzing solar activity

The Sun activity can be measured by counting the number of sunspots that appear each month. Periods of about 11 years are observed. The prediction of these cycles (or half-cycles…) is notoriously difficult. In order to test the algorithm and its ability to detect large-scale patterns, we are going to apply it to the long-term dynamic of the Sun. The algorithm is parameterized with the characteristic scale of 11 years: it will analyze the relation between 132 monthly measurements and the next 132 observations. Data is collected from the SILSO resource of the Royal Observatory of Belgium. The analysis script is available in my source repository.

3D representation of causal states, infered from solar cycle data. The image is dynamic and you can navigate through the structure. Years of solar maxima are noted in blue and minima in black.

The method proposes a projection of causal states on a reduced set of most relevant parameters. Clearly, the first two, X and Y, encode together the 11-year period as well as the phase along the cycle. Which is expected, given this is the main macroscopic feature of this process.

Trajectories seem to all fit on a conical structure. But what is the meaning of the Z parameter, coding for the height along the cone? This parameter is identified as important by the algorithm, which puts it in third position, but I could not figure out its signification. I thus asked experts from SILSO: this parameter captures the low-frequency modulation of the amplitudes known as the Gleissberg cycle. And, indeed, dates on the lower or higher ends of the cone match these of the low-frequency modulation. So, the algorithm has also captured a pattern on a scale that far exceeds its immediate temporal horizon of 132 months! This demonstrate its ability to encode the dynamics of the process, not just the immediate statistical dependencies.

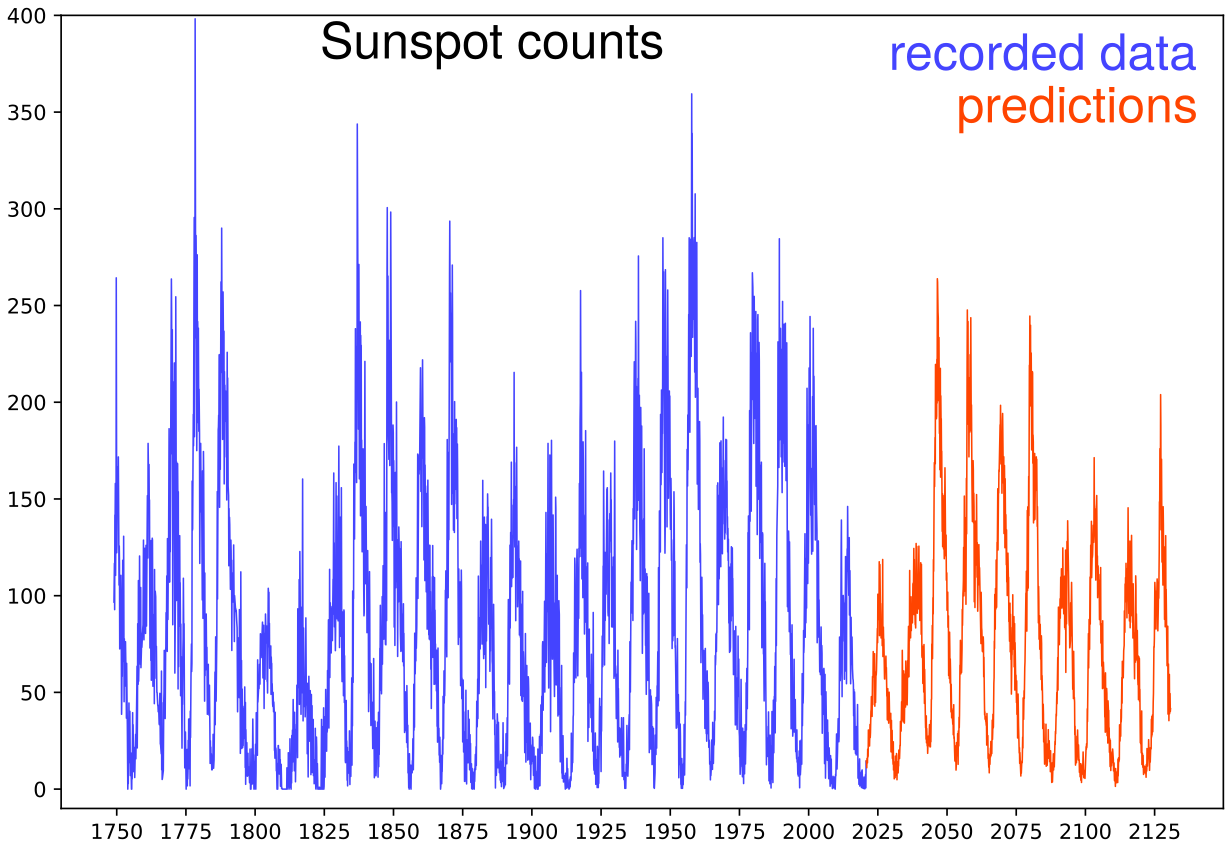
Predictions obtained by the method on a ridiculously long time frame. The idea is to show the general behavior of the algorithm, which produces a possible realization of the modeled process. There are maybe small issues with minima, but globally the cycles are well produced. The predicted series look plausible and consistent with the measured data. Including, the appearance of another Gleissberg cycle! Yet, given the well-known difficulty of this data set, it is illusory to give the slightest credit to predictions beyond one cycle. In terms of dynamical systems, the predictions just show a possible trajectory along the "attractor". One may ask how fast the initial information diffuses, how fast trajectories diverges, but this brings us too far for this illustrative example. A collaboration with experts of the domain would be necessary to calibrate the algorithm and analyze its ability to produce short term predictions.

Article and reference code

A preprint version of the article is available here, as well as on ArXiv.org.

The latest version of the source code is maintained here. The scripts are written in Python, with a C++ module used to improve computation times (a full-Python version is in preparation — please contact me if needed). There are no external dependencies, other than these provided together with the source code. MIT License: free to use for what you want, so long as you credit the author!