Présentation

Cet article introduit un nouvel algorithme pour reconstruire tant des epsilon-machines à partir des données que les états décisionnels. Ceux-ci sont définis comme les états internes d’un système qui donnent lieux aux mêmes prédictions, basées sur une fonction de coût/d’utilité fournie par l’utilisateur. Cette fonction encode une forme de connaissance a priori non présente dans le système, elle quantifie à quel point être exact ou se tromper sur les prédictions est utile ou néfaste. La structure intrinsèque du système est modélisée par une epsilon-machine et ses états causaux. Les états décisionnels forment une partition de ces états causaux dont la structure est définie à un plus haut niveau de description par la fonction d’utilité. Dans une perspective « Systèmes Complexes », les états décisionnels sont ainsi les structures « émergentes » correspondant à la fonction d’utilité. Le nouvel algorithme REMAPF estime à la fois la structure de l’epsilon-machine et des états décisionnels à partir des données, y compris leurs transitions. Des examples sont fournis : reconstruction d’automate markovien à partir de séries symboliques, filtrage dans des automates cellulaires, détection de bords dans des images.

Les contributions principales de cet article sont:

• Un algorithme pour calculer les états décisionnels à partir des données, qui comme étape étape intermédiaire reconstruit l’epsilon-machine.
• La façon dont l’information est encodée dans une fonction d’utilité, un moyen clair et nouveau pour introduire de la connaissance externe au système.
• Le fait de rassembler les états du système par classe d’équivalence amenant aux même décisions basées sur une fonction de coût/d’utilité.

Le code source de l'implémentation de référence est disponible comme logiciel Libre.

Vous trouverez également sur ce site un travail antérieur et voisin sur la mise à jour des états causaux dans un système en évolution.

Quelques détails

Prédictions dans un contexte physique

Dans un contexte physique le transfert d'information est limité par la vitesse de la lumière. Le « présent » d'un système est défini comme un seul point dans l'espace-temps. Ceci est à mettre en contraste avec les systèmes dynamiques, où le « présent » est constitué de l'intégralité du vecteur d'état (la ligne sur la figure ci-dessous). Dans le cas qui nous intéresse ici, il n'y a pas de propagation instantannée de l'information, et seule une petite partie du vecteur d'état est disponible.

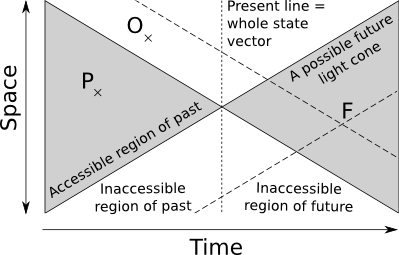
Le cône espace-temps passé est ici défini comme l'ensemble des points qui ait pu avoir une influence causale sur le présent. Le cône futur est de même défini comme l'ensemble des points ayant pu être influencés par le présent. Pour prédire correctement un point F dans le cône futur, il faut potentiellement disposer des points dans le cône passé de F. Alors qu'il est possible de disposer de certains d'entre eux comme P, dans le cône passé du système, le problème est que certains points comme O sont en dehors et non accessibles. Mais tant P que O font partie du cône passé de F, dans notre propre futur. La conséquence est que même pour un système déterministe on obtient une distribution statistique de futurs pour un passé observé donné. En d'autres termes, les conditions aux limites ou dans des régions inaccessibles peuvent déterminer une partie du futur.

Considérons maintenant le regroupement de deux cônes passés x₁^- et x₂^- s'ils ont la même distribution de futurs x⁺: p(x⁺|x₁^-)=p(x⁺|x₂^-). Supposons que le point P dans le passé ait une valeur différente pour les deux passés x₁^- et x₂^-. Il n'y a alors aucun moyen de retrouver quelle était la valeur de P par de nouvelles observations. On ne peut utiliser la connaissance obtenue dans le futur par ces observations pour décider entre x₁^- et x₂^- puisque p(x⁺|x₁^-)=p(x⁺|x₂^-). En pratique ces deux passés sont donc équivalents. Mathématiquement la relation d'équivalence associée x₁^- ≡ x₂^- partitionne le passé du système en ensembles σ(x^-)={ y^-: p(x⁺|y^-)=p(x⁺|x^-)}.

Les ensembles σ sont appelés les états causaux du système (cf Cosma Shalizi's Thesis). Dans un cadre discret une nouvelle observation donne lieu à une transition entre un état σ₁ et un état σ₂. Les états causaux et leurs transitions forment un automate déterministe, l'ε-machine (cf cet article par James Crutchfield and Karl Young). Un résultat intéressant est l'abstraction des dépendances du passé dans les états causaux. Les transitions entre les états incluent toutes les dépendances du passé pouvant avoir une influence sur le futur, et l'ε-machine forme en fait un graph Markovien.

La construction des états causaux n'est pas limitée aux cônes espace-temps. On peut également regrouper ensemble des données (paramètres) x∊X en fonction des distributions de probabilités conditionnelles p(z|x) pour des points z∊Z d'un espace de prédictions. La même relation d'équivalence peut alors être définie comme ci-dessus. Et on peut appeler états causaux les classes d'équivalence induites par cette relation par analogie (ou abus), même si aucune notion de causalité n'est alors explicitement introduite.

Introduction d'une fonction d'utilité

La description précédente ne distingue pas les futurs qui ont des conséquences importantes où anodines pour l'observateur. Par exemple, administrer un médicament à un patient peut causer des effets secondaires graves. L'approche des états causaux est de regarder p(effet|médicament), mais ne spécifie pas si l'effet est désiré ou non. En pratique on devrait tenir compte de nombreux paramètres comme l'état du patient quand on lui donne le médicament, etc. Il s'agit juste ici d'un exemple d'illustration où on veut prédire un effet (espace Z) à partir d'un médicament (espace X).

L'idée est alors d'introduire une fonction d'utilité U(y,z) pour quantifier la conséquence de prédire y∊Z (l'effet que l'on pense va se produire) alors qu'en fait c'est l'effet z qui apparaît. Par exemple, si on donne un médicament pour soigner le mal de tête mais que le patient se retrouve avec un mal au ventre en plus du mal de tête qui n'a pas disparu, alors l'utilité de la prédiction initiale n'est pas très bonne.

Que se passe-t'il si on regroupe maintenant les médicaments en tenant compte de leur utilité espérée E[U(effet|médicament)]=E[U(y|x)]=∫_z∊ZU(y,z)p(z|x) au lieu de simplement les probabilités conditionnelles p(effet|médicament) ? On peut alors:

• Regrouper x₁ et x₂ si l'effet d'utilité espérée maximale est le même. Ceci permet de classer les médicaments par catégorie, comme ceux pour le mal de tête et ceux pour le mal de ventre. Mais ça ne dit rien sur les effets secondaires.
• Regrouper x₁ et x₂ quand l'utilité maximale attendue est la même. Ceci permet de classer les médicaments en fonction de leur puissance, et éventuellement placer les plus puissants seulement sur ordonnance. Mais cela n'indique pas quel est l'effet attendu pour chaque médicament.
• Faire les deux à la fois.

En termes techniques:

• Le premier cas correspond à x₁ ≡ x₂ quand argmax_y∊ZE[U(y|x₁)]=argmax_y∊ZE[U(y|x₁)]. Les classes d'équivalence sont les états d'iso-prédiction.
• Le second cas correspond à x₁ ≡ x₂ quand max_y∊ZE[U(y|x₁)]=max_y∊ZE[U(y|x₁)]. Les classes d'équivalence sont les états d'iso-utilité.
• Le troisième cas correspond à l'intersection des deux premiers. Les classes d'équivalences sont les états décisionnels.

L'article donne plus de détails. Le nom "état décisionnel" vient de l'hypothèse que la fonction d'utilité encode tout ce que l'utilisateur à besoin de savoir pour prendre une décision.

Si comme supposé dans la thèse de Shalizi susmentionnée « les structures émergentes sont des sous-machines de l'ε-machine », alors une conséquence intéressante est que les états décisionnels sont les structures émergentes correspondantes à la fonction d'utilité. Une autre conséquence est que les transitions entre états décisionnels correspondent à des évènements du système qui provoquent un changement de décision. D'où la réponse au problème posé en introduction.

Relation entre les états décisionnels et l’epsilon-machine

Les états décisionnels rassemblent les causal states à un niveau plus élevé. Ils forment conséquemment une sous-machine de l’epsilon-machine:

Télécharger le code source

La version 1.0 est sortie ! Elle contient le code source pour les exemples donnés dans l’article ainsi que la documentation pour écrire vos propres programmes.

La version de développement est maintenue dans mon dépôt de sources. La dernière version du moment peut être téléchargée soit en tant qu'archive tar.gz, soit en utilisant GIT: git clone git://source.numerimoire.net/decisional_states.git.

L'implémentation de référence est disponible en logiciel libre aux termes de la GNU LGPL v2.1 ou plus récente.

Documentation du code (en Anglais)

Merci de vous reporter au document de référence (en anglais) pour la documentation complète. Vous trouverez ci-dessous un extrait de ce document.

Quick recipies for the impatient

If all you want is to try this code in place of CSSR just run the “SymbolicSeries” example. It will tell you what arguments it needs and will reconstruct an ε-machine out of your data.

Is your data a discrete time series, or can it be made discrete in an natural way? Then discretise it and run the “SymbolicSeries” example.

Is your data a continuous time series? Try the “TimeSeries” example and adapt the default parameters in the source code (past and future size, subsampling and Taken's style time-lag vectors, utility function). Pay attention in particular to the kernel width parameter, and not to under- or over- smooth your data. The best kernel width is usually determined a posteriori, not a priori. Say for example that you use the statistical complexity to discriminate between one kind of series and the others. The best kernel width is the one that gives the best discrimination accuracy, implicitly realizing the best bias/variance compromise for your specific problem, and not the kernel width that maximizes an a priori criterion like AMISE. You should thus explore a range of kernel width and optimize an a posteriori criterion. If you are not satisfied with the results try to apply a high-pass filter (even a bad one like first differences) or any detrending method. In fact the best results are obtained when the range taken by the data values doesn’t vary too much from the beginning to the end of the series. If nothing works or if you reach cpu or memory limits, try to discretize your series in a clever way and switch to the SymbolicSeries example.

Is your data spatial, or cast in a light-cone setup, or simply not a time series? See the image processing and the cellular automaton example and adapt them to your scenario. All you need is to cast your problem in a predictive framework: ex: Predict the center pixel from its neighbors. Then the equivalent of the “past” of the time series becomes the data you need for the prediction (ex: the neighbors in this case) and the “future” of the time series becomes the data you predict (ex: the center pixel in this case). The API is explicitly worded as “DataType” and “PredictionType” for this reason, not to be restricted to time series. You may even provide transitions and the associated symbols if you are in a discrete setup (see the CellularAutomaton for how to do that).

Do you want a Generative markov model relevant to your Utility function ? Then modify one of the above examples, you will have to implement your Utility function in C++. See section 4.4 of the documentation for how to do that.

What the code looks like: Step by step example

This section recapitulates the main points with a toy example. The scenario is of predicting whether it will be sunny or raining based on observations from the past 3 days. Based on this prediction we plan each day to uncover or keep shut a tent containing a collection of mirrors concentrating sun rays on a solar oven.

Let's first declare the data types and meta-parameters. We decide to encode the past three days state into a 3-bit field : 000 = rainy-rainy-rainy, 001 = rainy-rainy-sunny, … 111 = sunny-sunny-sunny. These values fit on an unsigned 8-bit integer. From this we wish to predict a boolean value, whether it will be sunny or not. We decide to store all observations in a vector. The data set can thus be defined:

typedef vector< pair<uint8_t, bool> > DataSet;

Given the nature of the data, we will simply invoke the default discrete distribution manager:

typedef DiscreteDistributionManager<DataSet> DistManager;

We have in this example a utility function. If we open the tent when it is sunny we can benefit from the solar oven, so we have utility(planned=sunny, real=sunny)=1. When we open the tent but it rains we do not benefit from the oven and we will have to clean up the mirrors in the evening, a costly operation, so utility(planned=sunny, real=rainy)=-1. When we keep the tent shut we gain nothing so we set a utility of 0. Let's define this function simply :

int utility(bool predicted, bool real) {
    if (predicted && real) return 1;
    if (predicted && !real) return -1;
    return 0;
}

In order to optimise the expected utility we can invoke the default exhaustive optimiser:

typedef ExhaustiveOptimiser< vector<bool> > Optimiser;

We have to provide to this object the range of all possible prediction values, in this case a vector containing two elements true and false. See Section 4.4.2 and the CellularAutomaton for a perhaps more elegant way of defining the optimiser. This is out of scope of the toy scenario.

Now let's define the main analyser object:

typedef DecisionalStatesAnalyser<DistributionManager, DataSet, Optimiser> Analyser;

We are done with the declarations of C++ types, and we can now build objects of these types:

DataSet dataset;
DistManager distManager(dataset);
vector<bool> all_predictions(2); all_predictions[0]=false; all_predictions[1]=true;
Optimiser optimiser(all_predictions);
Analyser analyser(distManager,dataset,optimiser);

Assuming you have filled the data set with your observations (ex: collected in a file), then we can compute the causal states :

analyser.computeCausalStates();

Then we can apply the utility function on top of these states:

analyser.applyUtility( &utility );

And now we can compute the iso-utility, iso-prediction, and finally the decisional states

analyser.computeIsoUtilityStates();
analyser.computeIsoPredictionStates();
analyser.computeDecisionalStates();

Note that we used the default clustering algorithm with default parameters, see Section 4.3.

We have computed the states, now is the time to do something with them. You could for example compute the statistical complexity of the system:

double C = analyser.statisticalComplexity();

Or perhaps, display the local decisional complexity values:

for (int i=0; i<dataset.size(); ++i) {
    uint8_t observed_state = dataset[i].first;
    cout << analyser.localDecisionalComplexity(observed_state) << endl;
}

See the examples provided with the source code for other uses, like filtering an image or writing the series of inferred states in a file.

One particularly interesting operation is to compute the ε-machine. But notice that in this toy scenario we did not so far introduce the notion of symbols. Since we have declared the data set using a standard vector container, we will provide the symbols here with a transition feeder (see Section 4.1.5).

struct TransitionFeeder {
    // we will simply access the data set elements by their indices
    typedef int iterator;
    iterator begin() { return 0; }
    // but the last transition is between the two last data set elements
    iterator end() { return dataset.size()-1; }
    
    // our constructor needs the data set reference
    DataSet& dataset;
    TransitionFeeder(DataSet& ds) : dataset(ds) {}

    // We assume the vector has no gap, all entries are transitions
    uint8_t getDataBeforeTransition(int idx) { return dataset[idx].first; }
    uint8_t getDataAfterTransition(int idx) { return dataset[idx+1].first; }

    // Now the interesting part. We will use text symbols as an illustration
    typedef char SymbolType;
    SymbolType getSymbol(int idx) {
        // Recall that we encoded the last 3 days as 3 bits: 000, 001, etc.
        // The emitted symbol corresponds to the last bit of the new day.
        // This is easily extracted with a bit mask (value AND 001)
        uint8_t symbol = getDataAfterTransition(idx) & 1;
        // we return the symbol as a character in this example
        if (symbol) return '1';
        return '0';
    }
};

Using this transition feeder is easy:

TransitionFeeder feeder(dataset);

And the above code for declaring the analyser now uses the transition feeder instead of the data set:

Analyser analyser(distManager,feeder,optimiser);

The causal states computation is done by calling analyser.computeCausalStates(); exactly as before, but the symbols are now taken into account for making the ε-machine deterministic. The ε-machine itself can be computed simply:

analyser.buildCausalStateGraph();

And we can write it on the standard output as a graph in the “dot” format:

analyser.writeCausalStateGraph(cout);

This simple toy scenario was designed to set you up quickly for using the main objects in your own code. Please see also the examples provided with the source code.